Beer Coaster Problem

The problem

Let there be two circular beer coasters of equal area. The two coasters are moved on top of each other such that the area of the overlapping region is half the area of any one of the coasters, as illustrated below: (Try hovering)

A
A
A/2

Give an algorithm, with the usual desirable properties and expressed as pseudocode, for solving the problem. The solution will include finding the angle a, as illustrated in the following figure.

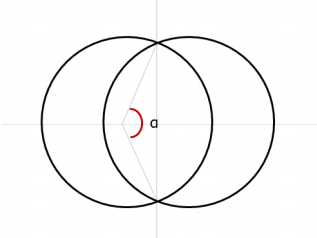
What we need to find

The solution

  1. If we consider just one circle, we can see that we need to find a segment of area 1/4 of the total area (figure 1) and multiply that by two for the entire overlap area. From there, maybe we can work backwards to get some information that will help us get to the angle.
    A/4
    Figure 1
  2. Wolfram Mathworld has an excellent explanation for solving the area of a circular segment which I won't go over again here, but the final formula boils down to:
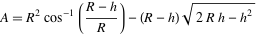
    Formula for the area of a circular segment
  3. Since we know that we are trying to find a circular segment equivalent to a quarter of the area of the circle, we can simply replace the 'A' in the LHS of the above formula with:
    A = 1/4 (Π * R2)
  4. Looking at the circular segment formula again with this new LHS value, we realize the only unknown value is h, the maximum height of the segment. Solving for h is not trivial, so I wrote a simple bruteforcer to find the value found below.
  5. Once h has been found, we can compute the length of half the chord (to find one side of the right-angled triangle.
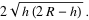
    chord = formula for a chord in the circular segment
    Half the chord is just the above without the leading '2'
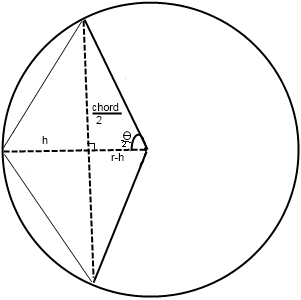
  6. As Figure 2 above shows, we now have half the length of the chord. The distance from the chord to the center of the circle can be found with a subtraction: r-h.
  7. Thinking back to high school trigonometry (SOH CAH TOA), we can find the unknown angle using the TOA part. Then multiply it by two to solve the problem.
    Angle = 2 * atan( halfChord / r-h)
  8. Now we rejoice.
    The angle is ~132degrees

The program

Demo

Pseudocode

// Finds the angle between the two equal sides of an isoceles triangle
// formed within a circular segment that has an area equal to 1/4th of the total circle's area

// Input: Circle's radius (optional*)
// Output: the height of the triangle and the angle between the two equal sides

r    <- user input radius
RHS  <- 0
LHS  <- (pi * r^2)/4
step <- 1.0
previousActionWasAdd <- true

while RHS != LHS
	if LHS > RHS
		if (previousActionWasAdd)
			height <- height + step
		else
			step <- step / 2
			height <- height + step
			previousActionWasAdd <- true

	if LHS < RHS
		if (previousActionWasAdd)
			step <- step / 2
			height <- height - step
			previousActionWasAdd <- false
		else
			height <- height - step


	// Calulcate the RHS based on the formula of a circular segment
	RHS = ( r^2*arccos((r-height)/r) ) - ( (r-height)*sqrt(2*r*height - height^2) );

// Now that we found the height, let's find the chord
halfChord <- sqrt( height * (2*r - height));

// Find r-h
distanceToCenter <- r - height;

// Find the angle times two
angle <- 2 * arctan(halfChord / distanceToCenter);

Actual code

function calculateAngle( radius ) {
	$('#demoOutput').html(''); // clear from last run

	// 1/4 of the area, rounded to 8 decimal places
	var LHS = (Math.PI * Math.pow(radius, 2)) / 4
	    LHS = round(LHS, 8);

	var RHS = 0.0;
	var height = 0.0;
	var step = 1.0;
	var previousActionWasAdd = true;
	var iterator = 0;

	$('#demoOutput').append("Brute forcing the height value");

	// Brute force to find what value of h makes the LHS == RHS
	while ( RHS != LHS ){

		if (iterator++ > 100) // Shouldn't loop this long
			break;

		// If h is too small
		if (LHS > RHS) {
			// If we added previously don't change the step
			if (previousActionWasAdd)
				height += step;
			// Otherwise, reduce the step by half and add it to h
			else {
				step /= 2;
				height += step;
				previousActionWasAdd = true;
			}
		// If h is too big
		} else if ( LHS < RHS ) {
			// If we added previous, reduce the step by half and subtract
			if (previousActionWasAdd){
				step /= 2;
				height -= step;
				previousActionWasAdd = false;
			// Otherwise, subtract again
			} else
				height -= step;

		}

		// Calulcate the RHS based on the formula of a circular segment
		RHS = Math.pow(radius,2) * Math.acos( (radius - height) / radius) -
			( radius - height) * Math.sqrt(2*radius*height
			- Math.pow(height, 2));

		// Round it to 8 decimal places
		RHS = round(RHS, 8);

		// Log our work
		$('#demoOutput').append('Iteration #'+iterator +
					' - Height = ' +
					height + 'LHS = ' +
					LHS+ 'RHS = ' +
					RHS + '');
	}

	// Now that we found the h, let's find the chord
	var halfChord = Math.sqrt( height * (2*radius - height));
	$('#demoOutput').append("Half the Cord is: " + halfChord);

	// Find r-h
	var distanceToCenter = radius - height;
	$('#demoOutput').append('radius - segmentHeight is: ' + distanceToCenter);

	// Find the angle times two
	var angle = 2 * Math.atan(halfChord / distanceToCenter);

	$('#demoOutput').append("Answer is: " +
			angle*(180/Math.PI) + " °, or " +
			angle + " radians.");
}

// This functions rounds a num to any given dec places
function round(num, dec) {
	return Math.round(num*Math.pow(10,dec))/Math.pow(10,dec);
}

The Footer

All the code for this can be found on my github.